ROFORMER: ENHANCED TRANSFORMER WITH ROTARYPOSITION EMBEDDING
Positional Embedding을 해야 하는 이유?
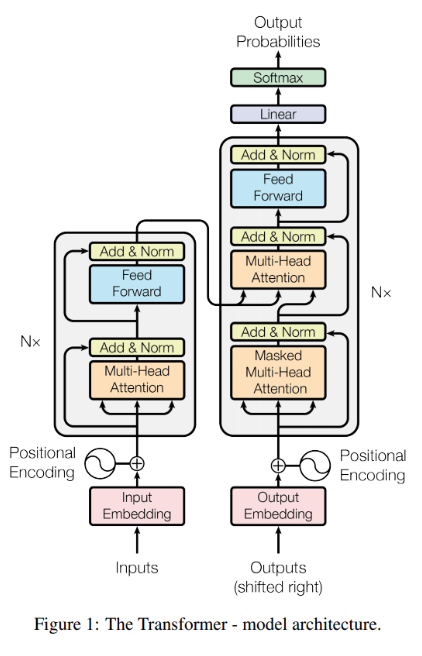
RNN, LSTM 구조와 같이 순환신경망에서는 단어의 순서 정보를 유지하고 있는 대신, 문장이길어질수록 앞 문장의 정보를 손실하게 되는 문제가 생긴다. 따라서, 이 문제를 해결할 수 있는 방법으로 Transformer가 등장했다.
이 Transformer는 attention이라는 개념을 도입하여문장의 순서와 관계없이 모든 문장의 정보들을 더해주어, 정보 손실의 우려가 없도록 한다.
또한, rnn구조와는 달리, 순차적으로 값을 계산하는 것이 아니라 병렬적으로 값을 처리하기 때문에 매우 빠르다.
다만, 병렬적으로 처리하다보니 문장의 순서에 대한 정보를 잊게 된다는 문제가 생긴다. 그래서 Transformer 논문에서는 Positional Encoding이라는 개념을 도입한다.
일반적으로 Positional Embedding 기법에는 크게 2가지로 나뉜다.
1. Absolute Position Embedding (APE) : Conv2s, BERT, ALBERT, GPT-1, GPT-2, ELECTRA
2. Relative Position Embedding (RPE) : Shaw's RPE, .., DeBERTa 등
APE 기법에 대해 알아보자.
앞서 말했다시피, APE는 input sequence의 절대적 위치를 input에 반영하는 방법이다.
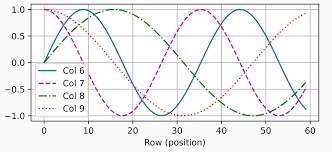
가장 기본적인 transformer에서는 positional ‘encoding’을 사용했는데
- 각 단어(token)의 위치마다 고유한 벡터를 만들어 내는 적절한 함수를 이용해,
- 문장에서 각 단어의 위치를 설명하는 위치 임베딩 벡터를 만든 뒤,
- 단어 임베딩 벡터에 더하는 방식으로 사용했다.

- x_i : token embedding
- p_i : position
- 주로 sin 함수와 cos 함수를 섞어서 사용한다.

이때 공주기만큼이 지나면 똑같은 주기가 반복되는데,
논문에서는 공주기가 돌아오기까지 길이가 문맥의 내용을 파악하는데 충분하다고 가정하고 사용한다.
RPE 기법에 대해 알아보자.
Shaw et al의 Self-Attention with Relative Position Representations 참고.
고정된 위치 정보를 제공하는 것이 아니라, 토큰 사이의 거리 정보를 활용하여 상대 위치 정보를 제공하는 방법이다.
(Distance Matrix를 사용하는 방법도 있으니, 참고하자!)
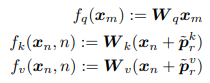
q.k.v에 위치 정보를 모두 제공하는 것이 아니라, k와 v에만 위치정보를 더한다.
- q^t*k 연산 전개식
앞선 식을 단순 전개하면 아래처럼 4개의 항이 나온다.

- x_m, x_n : m(n)번째 토큰 값
- W_q, W_k : weight matrix
- p_m , p_n : m(n)번째 위치 정보
첫 번째 항은 m번째 토큰과 n번째 토큰의 관계
두 번째 항은 m번째 토큰과 n번째 위치의 관계
세 번째 항은 m번째 위치와 n번째 토큰의 관계
네 번째 항은 m번째 위치와 n번째 위치의 관계
첫 번째 항은 두 단어의 의미적 차이를 학습하고, 두번째&세번째 항은 "지시대명사"를 학습하기 적합하다고 생각.
예를 들어, "I like potato. It is very delicious" 라는 문장에서 x_m : "potato" , x_n : "It" 일 때,
It 의 위치가 되는 p_n이 "potato"의 의미와 연결되지 않을까?
마지막 항에 대한 의미는 고찰 필요..
RPE 방식의 단점
- Attention Efficient 하지 않다.
- Attention 연산량이 4배로 늘었다.
따라서 아래는 연산량의 줄이기 위한 다양한 방법론들에 대해 몇 가지 설명하겠다.
Dai라는 저자는 위 식에서 약간의 변형을 시도했다.
아마, 마지막 항에서 두 토큰 간의 거리를 학습하는것에 대한 의문을 갖지 않았을까? 싶다.
그래서, p_m, p_n을 사용하지 않고, p_(m-n)을 사용하여 두 토큰의 거리를 한 번에 표현하고,
학습 가능한 파라미터 u, v를 사용했다. (u와 v는 한 번의 학습 과정을 거치고 fixed 된 값으로 사용한다.)

즉, n번째 단어는 u라는 값을 갖고, m-n 만큼 차이나는 거리를 갖는다면 v만큼의 값을 갖는다.
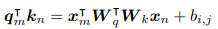
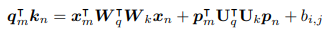
이렇듯, RPE 기법에는 이처럼 다양한 기법들이 존재한다!
RoPE 란 무엇인가?
Absolute 방식과 Relative 방식을 결합한 새로운 방법론!

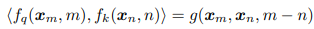
- 를 적용한 두 벡터의 내적이 반드시 의 관계식으로 표현할 수 있도록 해서 index의 차를 항상 반영하도록 하는 목적함수.
- q,k 를 position에 따라서 다른 각도로 rotation 시키는 방법이다.
RPE 에서 했던 방법과 동일하게, q와 k에만 위치 정보를 줄 것이다.
RE는 복소수의 실수 부분을 나타낸다.
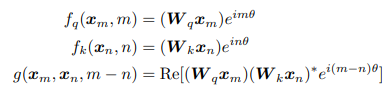
이렇게 rotary 방법을 사용하면, 두 벡터를 내적할 때 자연스럽게 (m-n) 에 dependent하게 된다.
- 바로 옆 토큰과는
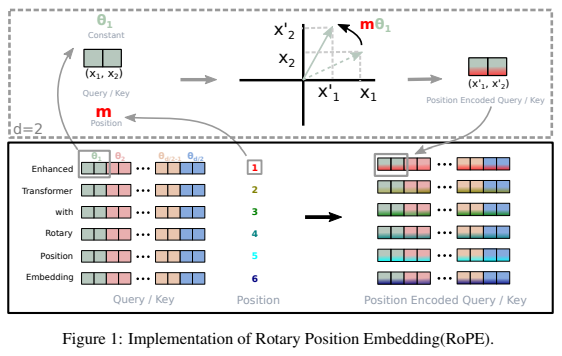
- d=2 인 경우를 생각해 보았을 때, 아래 처럼 나타낼 수 있다.
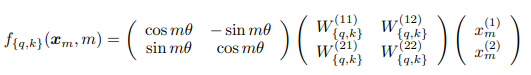
- 일반적인 경우,
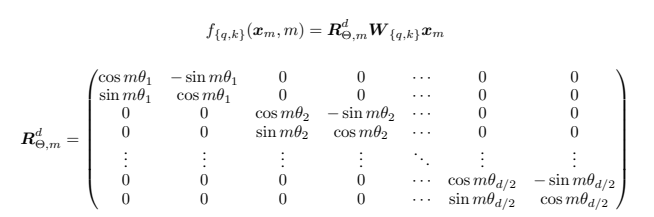
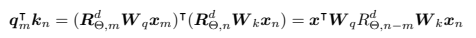
RoPE는 뭐가 새로울까?
기존의 RPE 방법과 비교해 보았을 때, 단순히 위치 정보를 sum 하는 것이 아니라
- 내적을 사용한다는 방법론적인 면에서 차별점이 있다.
왜 내적을 사용하는가?
단순히 sum을 했을 때에는 기존 단어의 의미론적 임베딩의 의미가 훼손될 우려가 있었다.
그리고, dot-product의 특성상 sequence의 길이가 길어질수록 값이 커지게 된다.
따라서 별도의 내적을 통해 위치 정보를 의미 훼손 없이 전달하고자 하는 시도였다고 할 수 있다.
- 또한 normalization을 할 때, normal 값이 항상 동일하므로 계산이 용이하다는 장점이 있다.
- Computational efficient realization of rotary matrix multiplication
- Long-term decay
실험 세팅 및 결과는 생략
Conclusion
Transformer 구조를 사용할 때 중요한 position embedding에 대한 새로운 기법.
APE+RPE 기법이라는 점이 인상적이다.